Equivalent

Description

This operation determines if two epsilon-free deterministic weighted acceptors are equivalent, that is if they accept the same strings with the same weights.

Usage

template <class Arc>
bool Equivalent(const Fst<Arc> &fst1,
                const Fst<Arc> &fst2,
                double delta = kDelta);

fstequivalent a.fst b.fst

Examples

A	B	C

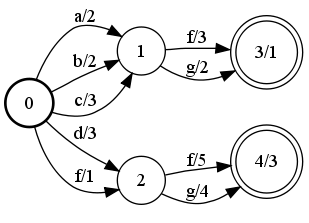
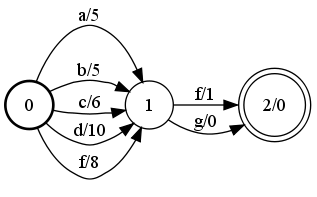
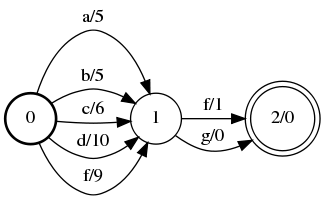
Equivalent(A, B);  // returns true
Equivalent(A, C);  // returns false

$ if fstequivalent a.fst b.fst; then echo true; else echo false; fi
true
$ if fstequivalent a.fst c.fst; then echo true; else echo false; fi
false

Complexity

Equivalent

• Time:
  • Unweighted: quasi-linear, i.e. O(d n G(n))
  • Weighted: complexity of unweighted + complexity of weight-pushing
• Space: linear, i.e. O(n + d)

Caveats

Weighted equivalence is sensitive to machine precision when using floating-point-based weights especially with non-integral values. Consider using RandEquivalent instead.

See Also

Equal, Isomorphic, RandEquivalent

References

• Alfred V. Aho, John E. Hopcroft, and Jeffrey D. Ullman. "The Design and Analysis of Computer Programs". Addison-Wesley, 1974.

-- CyrilAllauzen - 03 Mar 2009