ShortestDistance
Description
This operation computes the shortest distance from the initial state to every state (when
reverse is
false) or
from every state to the final states (when
reverse is
true). The
shortest distance from
p to
q is the
⊕-sum of the weights of all the paths between
p and
q.
The weights must be right (left) distributive if
reverse is
false (
true)
and
k -closed (i.e.,
1 ⊕
x ⊕
x 2 ⊕ ... ⊕
x k +1 =
1 ⊕
x ⊕
x 2 ⊕ ... ⊕
x k ) (valid for non-negative
TropicalWeight) or
k -closed when restricted to the automaton (valid for
TropicalWeight with no negative weight cycles).
Usage
template<class Arc>
void ShortestDistance(const Fst<Arc> &fst, vector<typename Arc::Weight> *distance, bool reverse = false);
|
fstshortestdistance [--opts] a.fst [distance.txt]
--reverse: type = bool, default = false
Perform in the reverse direction
|
Examples
A, over the tropical semiring:
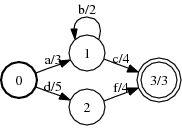
(TropicalWeight)
Shortest distance from the initial state
ShortestDistance(A, &distance);
fstshortestdistance a.fst
Shortest distance to the final states
ShortestDistance(A, &distance, true);
fstshortestdistance --reverse A.fst
Complexity
ShortestDistance:
- TIme:
- Acyclic: O(V + E)
- Cyclic:
- Tropical semiring: O(V log V + E)
- General: exponential
- Space: O(V)
where
V = # of states and
E = # of arcs.
Caveats
See
here for a discussion on efficient usage.
See Also
ShortestPath,
State Queues
References
--
CyrilAllauzen - 05 Jul 2007
 (TropicalWeight)
(TropicalWeight)
 , Journal of Automata, Languages and Combinatorics, 7(3):321-350, 2002.
, Journal of Automata, Languages and Combinatorics, 7(3):321-350, 2002.

